UPDATE: There is now a JavaScript Star Battle Solver! It’ll solve fairly simply ones no problem. Don’t expect miracles on harder puzzles, though — more likely than not they will just crash your browser.

This past weekend I “attended” my first MIT Mystery Hunt as part of Test Solution Please Ignore. I didn’t do much solving but what I did do was a lot of fun. Maybe I’ll attend in person next year; it’s always nice having an excuse to go to Boston.

Anyway, one member of our team designed a pretty cool logo:

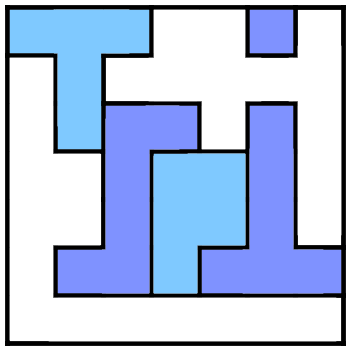
It’s a “TSPI”-themed star battle puzzle! You solve it by placing one star in each row, column, and region. I thought it was pretty cool, but I’m better at coding than solving, so I thought I’d write a quickie program in Python to solve it (and others). Here it is:

import numpy as np
# pip install python-constraint
from constraint import Problem

class StarBattle:
    '''
    A class for storing, solving, and printing star battle problems
    '''
    def __init__(self,matrix=None,stars=1):
        self.matrix = matrix
        self.stars = stars
        self.solutions = None
        
    def set_matrix(self,matrix):
        self.matrix=matrix
        
    def solve(self):
        M = self.matrix
        problem = Problem()
        
        myvars = np.unique(M)
        
        # The variables are the elements in the matrix
        # The domain for each variable is where it can be
        def where(M,i):
            coords = np.array(np.where(np.isin(M,i))).T
            return [tuple(j) for j in coords]
        
        for i in myvars:
            problem.addVariable(i,where(M,i))
        
        def is_not_adjacent(xy1,xy2):
            # Return true if two stars are not adjacent, in the same row, or same column.
            x1,y1 = xy1; x2,y2 = xy2
            if abs((x2-x1)*(y2-y1)) <= 1:
                return False
            else:
                return True
            
        # Problem constraints
        for i in myvars:
            for j in myvars:
                if i < j:
                    problem.addConstraint(is_not_adjacent,(i,j))

        self.solutions = problem.getSolutions()
        
    def display_solutions(self):
        # This is an ugly but effective way to display solutions
        # DIsplay
        if self.solutions is not None:
            for s in self.solutions:
                N = np.zeros_like(self.matrix)
                for k,v in s.iteritems():
                    N[v] = 1
                print N
                print
    
    def display(self):
        print self.matrix
#END class StarBattle

if __name__ == '__main__':
    M = np.array([
    [0,0,0,1,1,2,1],
    [3,0,1,1,1,1,1],
    [3,0,4,4,1,6,1],
    [3,3,4,5,5,6,1],
    [3,3,4,5,5,6,1],
    [3,4,4,5,6,6,6],
    [3,3,3,3,3,3,3]
    ])

    star_battle = StarBattle()
    star_battle.set_matrix(M)
    star_battle.display()
    print
    star_battle.solve()
    star_battle.display_solutions()

This works very fast, so I'm happy with it. It also gave me a chance to learn about the python-constraint library. However, there are two things I'd like to do to improve it.

(1) Star battle puzzles with a single star in each row, column, and region are easily solved above. But what about more advanced ones, with two or more stars? I'm not sure how to rewrite the code to do that, and I'd like to.

(2) Python is fine, but ideally this would be done in JavaScript so people could solve in their browsers. There's a port of the Python library in JavaScript so I feel the code should ideally be written there.

Any takers to help solve either of these issues?